
Bayesian Neural Networks (BNNs) represent a fusion of two powerful concepts in machine learning: neural networks and Bayesian inference. While traditional neural networks are deterministic and lack a natural way to account for uncertainty, Bayesian Neural Networks introduce a probabilistic framework that allows for the representation of uncertainty in both the model parameters and predictions.
In a Bayesian Neural Network, instead of having fixed weights as in a standard neural network, the weights are treated as probability distributions. This means that rather than providing a single point estimate for each weight, the model captures a range of possible values, expressing the inherent uncertainty in the parameters. We will look at a derivation of a simple neural networks, and the code implementation of this concept.
Derivation
Let us the regression problem of predicting a continuous target variable $t$ from a vector $\mathbf{x}$ of inputs. We will assume that the conditional distribution $p(t | \mathbf{x})$ is Gaussian, with the mean given by the output of a neural network model $y(\mathbf{x}, \mathbf{w})$, and with precision $\beta$. More concretely, we have that $$p(t | \mathbf{x}, \mathbf{w}, \beta) = N(t | y(\mathbf{x}, \mathbf{w}), \beta^{-1})$$
We choose a prior distribution on the weights $\mathbf{w}$, which is a multivariate Gaussian with precision matrix $\alpha \mathbf{I}$. More specifically, $$p(\mathbf{w} | \alpha) = N(\mathbf{w} | \mathbf{0}, \alpha^{-1} \mathbf{I})$$ The likelihood for the dataset is $$p(D | \mathbf{w}, \beta) = \prod_{n=1}^N N(t_n | y(\mathbf{x}_n, \mathbf{w}), \beta^{-1})$$ From the prior and the likelihood, we can calculate the posterior distribution of $\mathbf{w}$ $$p(\mathbf{w} | D, \alpha, \beta) \propto p(\mathbf{w} | \alpha) \, p(D | \mathbf{w}, \beta)$$ In the case of Bayesian Linear Regression, where $y(\mathbf{x}, \mathbf{w})$ is a linear function of $\mathbf{w}$, this quantity turns out to be Gaussian. However, in a neural network, where $y(\mathbf{x}, \mathbf{w})$ is an arbitrary function $\mathbf{w}$, the posterior will likely be non-Gaussian
Laplace Approximation
We can approximate the posterior of $\mathbf{w}$ using Laplace approximation, which involves finding a local minima, $\mathbf{w}_{MAP}$, of the log posterior $$\ln p(\mathbf{w} | D) = – \cfrac{\alpha}{2} \mathbf{w}^T\mathbf{w} \, – \, \cfrac{\beta}{2} \sum_{n=1}^N \{ y(\mathbf{x}_n, \mathbf{w}) \, – \, t_n \}^2 + \text{const}$$ This is only a local minima because the function is not guaranteed to be convex, like in the case of linear regression.
Having found a mode $\mathbf{w}_{MAP}$, we can then build a local Gaussian approximation by evaluating the matrix of second derivatives of the negative log posterior distribution. The value is calculated using $$\mathbf{A} = – \nabla_{\mathbf{w}}^2 \ln p(\mathbf{w} | D) = \alpha \mathbf{I} + \beta \mathbf{H}$$ where $\mathbf{H}$ is the Hessian matrix comprising the second derivatives of the sum-of-squares error function with respect to the components of $\mathbf{w}$. We can approximate the value of $\mathbf{H}$ using methods discussed in upcoming sections. Once we have found $\mathbf{A}$, the approximated posterior distribution of $\mathbf{w}$ is $$q(\mathbf{w} | D) = N(\mathbf{w} | \mathbf{w}_{MAP}, \mathbf{A}^{-1})$$ The predictive distribution is calculated by “averaging” over $\mathbf{w}$: $$p(t | \mathbf{x}, D, \alpha, \beta) = \int p(t | \mathbf{w}, \mathbf{x}, \beta) \, p(\mathbf{w} | D, \alpha) d \mathbf{w}$$ Even with the Gaussian approximation to the posterior, this integration is still analytically intractable because $y(\mathbf{x}, \mathbf{w})$ may not be linear.
To handle this, we approximate the value of $y(\mathbf{x}, \mathbf{w})$ using $$y(\mathbf{x}, \mathbf{w}) \simeq y(\mathbf{x}, \mathbf{w}_{MAP}) + \mathbf{g}^T (\mathbf{w} \,-\, \mathbf{w}_{MAP})$$ where $\mathbf{g} = \nabla_{\mathbf{w}} y(\mathbf{x}, \mathbf{w})$ evaluated at $\mathbf{w}_{MAP}$.
Using the property of Gaussian distribution, we see that the predictive distribution, under this assumption becomes $$p(t | \mathbf{x}, D, \alpha, \beta) = N(t | y(\mathbf{x}, \mathbf{w}_{MAP}), \sigma^2(x))$$ where $\sigma^2(x) = \beta^{-1} + \mathbf{g}^T \mathbf{A}^{-1} \mathbf{g}$
Diagonal approximation of the Hessian $\mathbf{H}$
In this section, we will look at ways to approximate the Hessian $\mathbf{H}$ using a method called diagonal approximation. This method simply replaces the off-diagonal elements with zeros, so that the inverse of $\mathbf{H}$ is trivial to calculate.
Let us consider an error function that consists of a sum of term, one for each pattern in the dataset. For the regression case, this may be the squared error. The Hessian can then be obtained by considering one pattern at a time, and then summing the results over all patterns. For one term $E_n$, we can see that $$\cfrac{\partial^2 E_n}{\partial w_{ji}^2} = \cfrac{\partial^2 E_n}{\partial a_{j}^2} z_i ^ 2$$ To calculate the first term on the right hand side, first see that $$\cfrac{\partial E_n}{\partial a_j} = h'(a_j) \sum_{k} \cfrac{\partial E_n}{\partial a_k} w_{kj}$$ where $k$ are the units on the next layer of the network. Take the derivative again w.r.t $a_j$, and eliminate the off-diagonal terms of the Hessian, we have that $$\cfrac{\partial^2 E_n}{\partial a_{j}^2} = h'(a_j)^2 \sum_{k} w_{kj}^2 \cfrac{\partial^2 E_n}{\partial a_k^2} + h”(a_j) \sum_{k} w_{kj} \cfrac{\partial E_n}{\partial a_k}$$ With this formula, we can obtain the approximated Hessian using an algorithm similar to back-propagation.
Python Implementation
We will implement a simple 2-layer Bayesian neural network with sigmoid activation function to calculate the sinusoidal function. The code implementation is available https://github.com/SonPhatTranDeveloper/bayesian-neural-network
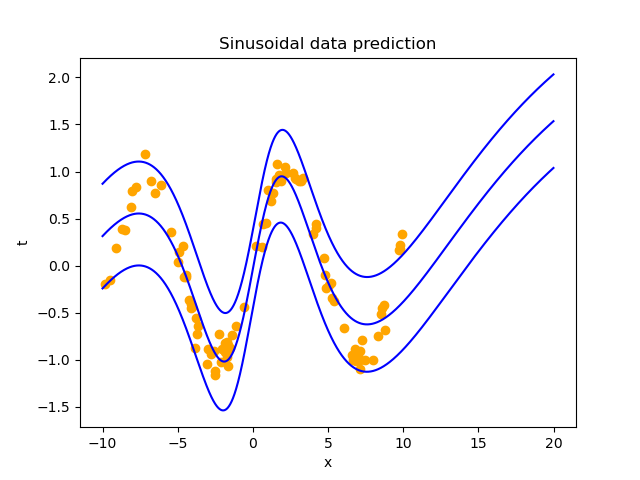
Below is the implementation of Bayesian Neural Network, with Hessian diagonal approximation
class BayesianNeuralNetwork:
def __init__(self, input_size, hidden_size, alpha, beta):
"""
Create a two-layer neural network
NOTE:
- The network does not include any bias b
- The network uses the sigmoid activation function
:param input_size: size of the input vector
:param hidden_size: size of the hidden layer
:param alpha: the prior precision of W
:param beta: the likelihood precision of t
"""
# Cache the size
self.input_size = input_size
self.hidden_size = hidden_size
# Cache the prior variance
self.alpha = alpha
self.beta = beta
# Create the layer
self.W1 = np.random.normal(size=(self.input_size, self.hidden_size))
self.W2 = np.random.normal(size=(self.hidden_size, 1))
# Create a cache
self.cache = {}
def forward(self, x_train, y_train):
"""
Perform the forward pass of the neural network
:param x_train: the training input of the neural network
:param y_train: the training
:return: the output of the neural network
"""
# Calculate the output of the first layer
a1 = x_train @ self.W1
z1 = sigmoid(a1)
# Calculate the output of the second layer
a2 = z1 @ self.W2
# Cache the values
self.cache = {
"x_train": x_train,
"y_train": y_train,
"a1": a1,
"z1": z1,
"a2": a2
}
# Calculate the error function
score = (1 / 2) * np.sum((y_train.reshape(-1) - a2.reshape(-1)) ** 2) / y_train.shape[0] \
+ (1 / 2) * np.sum(self.W1 ** 2) + (1 / 2) * np.sum(self.W2 ** 2)
return a2, score
def predict(self, x_test_points, x_train, y_train):
"""
Make full prediction, mean and variance for a datapoint
:param x_test_points: the test datapoints
:return: the predictions, mean and variance
"""
# Hold the mean and variance
means, variances = [], []
# Get the Hessian w.r.t W1 and W2
h_W1, h_W2 = self._get_hessian(x_train, y_train)
h_W = np.append(h_W1, h_W2)
A = self.alpha * np.ones(h_W1.shape[0] + h_W2.shape[0]) + self.beta * h_W
# Go through each test points
for x_test in x_test_points:
# Reshape x test
x_test = x_test.reshape(-1, 1)
# Calculate the mean
y, d_W1, d_W2 = self._get_gradients_w_map(x_test)
# Calculate the variance
d_W = np.append(d_W1, d_W2)
variance = (1 / self.beta) + np.dot(d_W, d_W / A)
# Append the mean and variance
means.append(y[0])
variances.append(variance)
return np.array(means).reshape(-1), np.array(variances).reshape(-1)
def _get_gradients_w_map(self, x_test):
"""
Get the gradient of the neural network with respect to the weights
:param x_test: the test data point
:return: the gradient with respect to the weights, with the prediction
"""
# Calculate the output of the first layer
a1 = x_test @ self.W1
z1 = sigmoid(a1)
# Calculate the output of the second layer
a2 = z1 @ self.W2
# Calculate the gradient w.r.t W1 and W2
d_a2 = np.ones_like(a2)
# Calculate the gradient w.r.t z1
d_z1 = d_a2 @ self.W2.T
# Calculate the gradient w.r.t W2
d_W2 = z1.T @ d_a2
# Calculate the gradient w.r.t a1
d_a1 = d_z1 * sigmoid_derivative(a1)
# Calculate the gradient w.r.t W1
d_W1 = x_test.T @ d_a1
return a2, d_W1, d_W2
def _get_hessian(self, x_train, y_train):
"""
Get the Hessian of the neural network w.r.t to W1 and W2
:param x_train: Training features
:param y_train: Training labels
:return: the Hessian w.r.t to W1 and W2
"""
# Perform forward propagation
self.forward(x_train, y_train)
# Get the w_map
W1, W2 = self.W1, self.W2
# Get the cached variables
x_train, y_train, a1, z1, a2 = self.cache["x_train"], self.cache["y_train"], \
self.cache["a1"], self.cache["z1"], self.cache["a2"]
# Get the number of training examples
N = x_train.shape[0]
# Calculate the diagonal Hessian w.r.t W2
h_W2 = np.sum(z1 ** 2, axis=0)
# Calculate the diagonal Hessian w.r.t W1
derivative_a = sigmoid_derivative(a1)
second_derivative_a = sigmoid_second_derivative(a1)
W2_repeat = np.repeat(W2.reshape(1, -1), N, axis=0)
h_a1 = ((derivative_a ** 2) * (W2_repeat ** 2) +
second_derivative_a * W2_repeat * (a2.reshape(-1) - y_train.reshape(-1)).reshape(-1, 1))
h_W1 = (x_train ** 2).T @ h_a1
# Return the Hessian w.r.t W1 and W2
return h_W1.reshape(-1), h_W2.reshape(-1)
def backward(self, learning_rate):
"""
Perform back-propagation
:param learning_rate: Learning rate of back-propagation
:return: None
"""
# Get cached values
x_train, y_train, a1, z1, a2 = self.cache["x_train"], self.cache["y_train"], \
self.cache["a1"], self.cache["z1"], self.cache["a2"]
# Calculate the gradient w.r.t a2
d_a2 = self.beta * (a2 - y_train.reshape(-1, 1)).reshape(-1, 1)
# Calculate the gradient w.r.t z1
d_z1 = d_a2 @ self.W2.T
# Calculate the gradient w.r.t W2
d_W2 = z1.T @ d_a2 + self.alpha * self.W2
# Calculate the gradient w.r.t a1
d_a1 = d_z1 * sigmoid_derivative(a1)
# Calculate the gradient w.r.t W1
d_W1 = x_train.T @ d_a1 + self.alpha * self.W1
# Perform back-prop
self.W1 -= learning_rate * d_W1
self.W2 -= learning_rate * d_W2